| Back |
|---|
Some Examples
As an aid to understanding the workings of simple relationships like Ohm’s Law, the analogy of water flowing through a pipe is often used and taught. In this, the quantity of water, (say in gallons), is analogous to the quantity of electrical charge, (in Coulombs). The rate of flow of water, (say in gallons per second past a certain point), is analogous to current, (measured in Coulombs per second or Amps). A water pipe becomes a wire; a rather ‘thin’ or small diameter pipe becomes a resistor and water pressure, (in pounds per square inch, or height or ‘Head of water’), becomes Volts. Extending the analogy further, a water pump is a fair analogy for a battery, and a parallel sided water tank for a capacitor. Unfortunately, there isn’t a very good analogy for a transistor, where a small water flow controls a larger water flow. Probably, the nearest to it is a tap where water flow is controlled by turning the tap handle. However, it must always be born in mind that analogies only help to explain some aspects of behaviour. For example, if you cut a water pipe, water gushes out, but if you cut a wire in an electrical circuit electrons don’t pour out. Electricity needs a complete circuit from “positive” to “negative” to flow. The analogy fails in this case.
Even our cherished model of the atom, with a positive charge crammed into a tiny space at its centre, surrounded by negatively charged electrons in orbits rather like our sun and its planets is a satisfying analogy which we know can’t really be true. Electrons circulating in orbits would radiate so we have to “modify” the analogy so that the electrons can only have fixed energy levels, (quanta), and therefore fixed orbits. Even if they could be in orbit, and we apply the same physics as applies to the sun and planets, (i.e. for stable orbits balancing their attraction to the nucleus with their centrifugal force), we find that the electrons in the inner orbits would have to be going round at faster than the speed of light! Again, it’s a case of “certain analogies to explain certain phenomena and others to explain others”. A rather unsatisfactory state of affairs! Never mind: science is more about understanding how things behave than about what things actually are.
Lines of electric and magnetic field are another example of using our imagination to create an analogy. Magnetic field lines, (or lines of force as they are sometimes called), shown by sprinkling iron filings onto a piece of paper held above a bar or horse-shoe magnet are the easiest to demonstrate and are often shown to school science classes. Electric field lines are more difficult to demonstrate but are frequently drawn to show the field of influence of electric charges when talking about electrostatics and they are equally valuable. However, it is important to remember that they are just analogies. They are no more real than the lines of latitude and longitude on the surface of the earth. Neither actually exist but they help our understanding and enable us to make predictions. At any point, an electric field line (or line of force), represents the direction that a positive charge would move in if placed at that point. However, they are not vectors. A true vector would indicate the strength of the field at a point by its length and the direction of the field by its direction. Field lines indicate the direction correctly but they usually indicate the strength of the field by their closeness or density. Arrow heads are assigned to field lines and convention dictates that the arrows point away from positive and towards negative charges in the electric case, and away from the North pole and towards the South pole of a magnet in the magnetic case. Take for example the electric field emanating from a point positive charge or a charged sphere as shown in figure 1. In our imagination we must treat field lines as if they dislike each other and take the easiest route to get away from each other. If an uncharged conductor is placed near a charge, some of the field lines bend towards it as indicated in Figure 2. This is exactly the same as if there were a negative charge placed the same distance behind the conductive surface as the positive charge is placed in front of it.
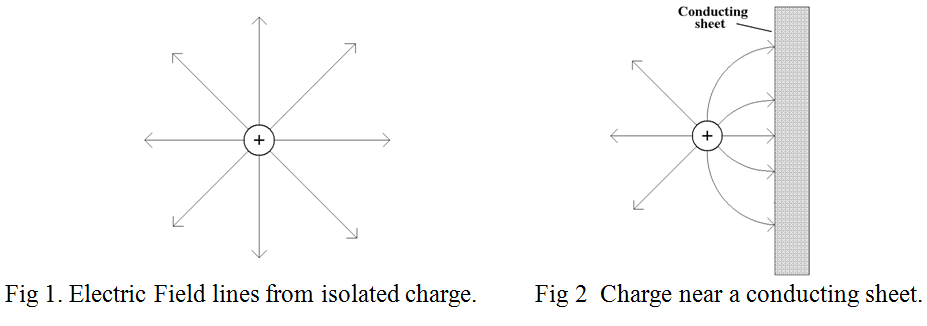
Field lines always contact a conducting surface at right angles to it. With dielectric surfaces it’s more complicated. It also helps to imagine field lines as if they behaved as springy steel wires. Any bending from their “free state” original course implies a physical (mechanical), force. The more the bending, the more the force. This applies to both electric and magnetic field lines.
Propagating E-M waves
Because electric charges and magnets always give rise to their respective fields and their imagined field lines, it might be thought that electric fields always emanate from electric charges, and magnetic fields always from magnets, but this is not always the case. An electric current forms a closed loop magnetic field around it and a propagating Electro-Magnetic wave can have electric field lines which do not necessarily terminate on a charge. In this case, (according to the theory), a mysterious and somewhat mythical electric charge has to be imagined called “electric displacement”. This is measured in coulombs per square metre and is beloved by those who understand Maxwell’s famous “Curl equations”. (Maxwell’s Curl equations are a pair of simultaneous differential equations which relate the shape of a wave in time to its shape in space, and the word “Curl” was first coined in this context, by Maxwell in 1873 to describe a particular vector operator. It has since become widely accepted). However, pursuing that is beyond the scope of this article.
Attraction and repulsion
We are taught in school that unlike charges attract each other and like charges repel. However, there is an alternative theory. This states that there is no such thing as a force of repulsion but only attraction. An isolated charge experiences no force in any direction because all the lines of force from it terminate on earthed objects a long way away, resulting in attraction in all directions equally. The presence of a second like charge “screens” the earthed objects in its direction by its own lines of force, resulting in a force on the first charge away from the second charge, hence looking like repulsion. This may be a valid alternative theory but it is more complicated than the one taught in schools, and it makes it more difficult to explain the “Inverse Square Law with distance” between the charges. It is much simpler to assume the “like charges rappel” theory because it adequately explains all the observed phenomena and is conceptually simpler. After all, “If it walks like a duck and quacks like a duck, it probably etc…”.
Next time we will look at some of the ways that these imaginary field lines can be used to connect electricity with magnetism.
| Back |
|---|
PRAECEPTOR