| Back |
|---|
Magnetic field
We are probably more familiar with static magnetic fields because most of us have, at some time or other, played with permanent magnets. Just like the electric fields described above, magnetic fields can also be visualised as “lines of force”, and most people will have seen the beautiful field patterns displayed by sprinkling iron filings onto a piece of paper above a “horseshoe” or “bar” magnet. An electric current also generates a magnetic field. Even a straight wire carrying a current generates a magnetic field and the lines of force surround the wire as shown in figure 2a. A single “turn” of wire generates lines of force, all of which go through the turn or coil and complete their “magnetic circuit” outside the coil as shown in figure 2b.
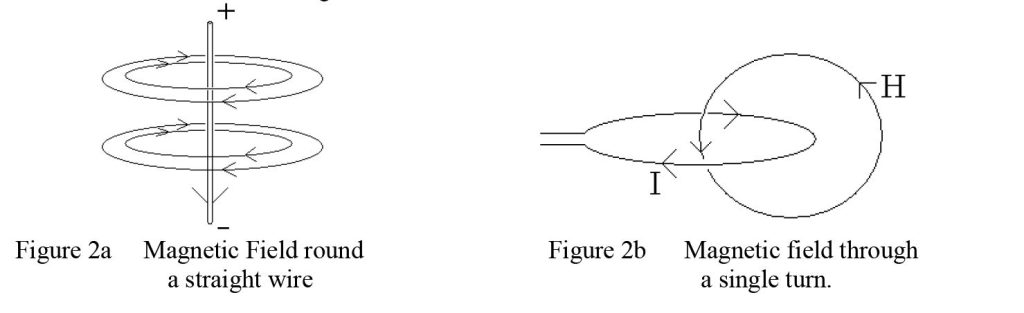
These figures only show one or two curved lines representing the magnetic field. You must imagine lots of them, closer together where the field is stronger, (say nearer the wire in figure 2a, and through the turn in figure 2b), and spreading out more thinly at greater distances.
Although I have considered a constant electric current and therefore a static magnetic field for simplicity, exactly the same reasoning would apply if, say, 2 Amps RMS of RF were passed through the wire. The magnetic field would then alternate at the RF frequency.
Magnetic field at a distance from a loop is a little more difficult to calculate, than the case of the uniform electric field between parallel plates, but is easily imagined. In the configuration of figure 2b, imagine the curved and closed magnetic line of force, which is just 1 metre in circumference. With 2 amps flowing in the loop, the Magnetic field strength along this curved line would be 2 Amps per metre.
If you choose a magnetic line of force of greater length, the magnetic field strength would be correspondingly less. Magnetic Field Strength is actually the rate of change of magnetic potential measured along the field line, but for this elementary explanation, we do not need to understand magnetic potential, except to say that it is the magnetic equivalent of Volts as measured along an electric field line.
Incidentally, if the coil consisted of 2 turns, the same current will of course travel through both turns, and the magnetic field in the above example would then be 4 Amps per metre. The strength of an electro-magnet is just determined by the current in Amps times the number of turns. I.e. 100 Amps through a single turn produces the same magnetic field in shape and strength as 1 Amp through 100 turns, (but you must assume the same geometry, i.e. the 100 turns must be squeezed into the same space as the single turn). However, because “turns” has no dimensions, it does not figure in the resulting units of strength of the magnetic field. “Turns” is a sort of hidden unit, because it is just a number. Hidden units often give rise to confusion for the unwary, as we shall see later. Incidentally, “Magnetic Field” is actually defined in terms of the force, (in Newtons), exerted on a unit Magnetic Pole, (which does not exist in practice), in the uniform magnetic field. However, this rather impractical definition need not concern us here. The next article looks at the electro-magnetic properties of materials.
| Back |
|---|
