| Back |
|---|
Impedance of Free Space is a difficult concept for ordinary electrical engineers because we all know that, at DC, the impedance between a pair of separated wires looks like an Open Circuit, or in other words the impedance is infinite. However, it has some very practical applications as we shall see in a later article. But first, we must be completely familiar with what is meant by Electric and Magnetic fields, so the first two articles are something of a recap. Let me start with some things which all Radio Amateurs are familiar with.
We should be familiar with what is meant by “The Characteristic Impedance of a transmission line”.
a) It is the ratio of “electrical pressure” or voltage on the transmission line to the resulting flow of current in the line, also,
b) It is the value of resistance which, when placed across the far end of the transmission line, absorbs all the power sent into the near end of the line with no reflection from the far end.
The ratio of Volts divided by Amps is given a new unit called Ohms, so when ever we see a result which has the “Dimensions” or “units” of Volts/Amps we can substitute “Ohms”.
In empty space, there are no wires to have a voltage on them or current through them, instead space may support an electric field and a magnetic field. This is a slightly more difficult concept (which I will say more about later). Whereas a wire may be regarded as one dimensional, space should be regarded as three dimensional.
The proper definition of the impedance of free space is that it is the ratio of the electric to magnetic fields in that space. The rather trite answer to its value, and the units it is measured in, (which, although true, doesn’t help our real understanding much), is that, electric field is measured in Volts per metre, and magnetic field is measured in amps per metre, so the ratio of volts per metre divided by amps per metre is Ohms. The numerical value could, in principle, be determined by setting up a measuring system in the far field of a transmitter and aerial and measuring the electric field with a pair of probes, and the magnetic field with a loop at the same position. However, before pursuing this rather trite answer and doing an experiment, let us be sure that we really understand what are meant by electric and magnetic fields.
A comprehensive treatment of this subject normally takes a full university term of lectures, so in the following, please excuse my gross over-simplification.
Electric field.
Imagine a pair of large square metal plates, each of area equal and to the area occupied by your house. The lower plate is resting on the ground and is effectively earthed. The upper plate is two metres above the lower and a 10 Volt battery is connected between the plates as indicated by figure 1. An electric field is said to exist between the plates which may be represented by “lines of force” shown dotted in figure 1. I have only shown them along the near edge of the plates, but you have to imagine them filling the space between the plates. Note that the lines of force are slightly curved at the edges of the plates, but are virtually parallel away from the edges. Remember also that these lines are purely imaginary, (just as lines of latitude and longitude are on the surface of the earth), but they help us to visualise the situation. We must also imagine that the higher the voltage between the plates, the more crowded are the lines of force, and so the more intense is the electric field. In this example, with 10 volts between the plates, and 2 metre plate separation, the static electric field where the field lines are parallel, (away from the edges), is 5 volts per metre.
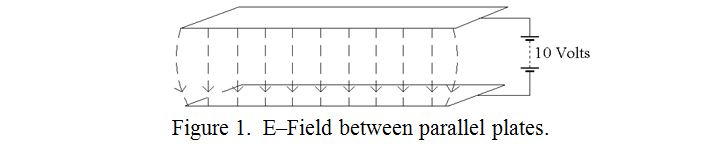
Although I have considered a static electric field for simplicity, exactly the same reasoning would apply if 10 volts RMS of RF were applied. The field between the plates would then be 5 volts RMS per metre.
If you stood between the plates, you wouldn’t feel anything as this is quite a small field in terms of our senses, but it is quite a large field for a neighbour’s TV aerial to stand without considerable interference! Also, when you stand between the plates, you alter the field. In fact, if you are 1.75 metres tall and a good electrical conductor, the field above your head would be 10/0.25, or 40 volts per metre. This would not be enough to make your hair stand on end. You need in the order of 105 volts per metre to do this!
Fundamentally, “Electric field” is actually defined in terms of the force, (in Newtons), exerted on a unit charge, (1 coulomb), in the uniform electric field. But this is a rather impractical definition and need not concern us here. So much for the introduction to electric fields.
In the next part, we will look at magnetic fields.
| Back |
|---|
John, G0NVZ