Back

In “radio science”, ‘Q’ stands for Quality factor. In a simple resonant or tuned circuit, (and indeed also in a single inductor or capacitor), Q is conveniently summarised as “the component’s reactance divided by the component’s resistance”. The higher the Q, the lower the loss in the component’s resistance. (In most tuned circuits it is usually assumed that capacitors are relatively perfect compared to inductors). Thus, the Q of a tuned circuit is virtually the Q of the inductor. By some mathematical trickery, Q also determines the magnification factor between the voltage you feed in, (in series with the inductor and capacitor of a tuned circuit at resonance), and the voltage you get out across either the inductor or the capacitor alone. How does this voltage magnification come about without the aid of a transformer?

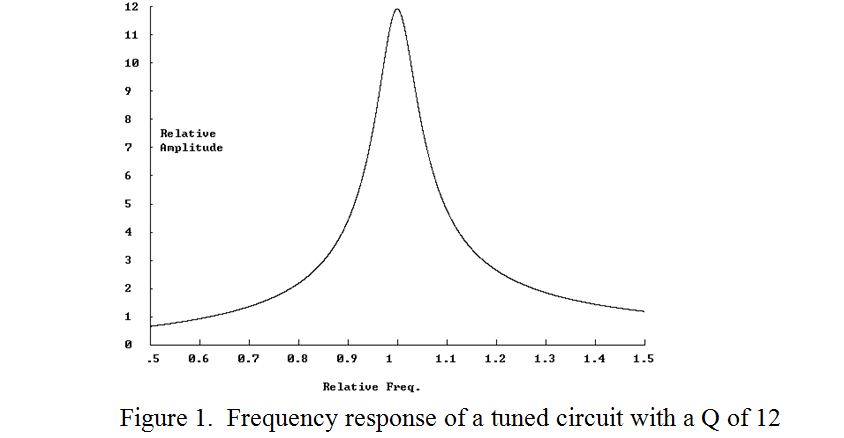
Basically it is a matter of persuading a modest current to flow through a high impedance. To understand this we have to go back to Ohms law, where V=IR, or in this case V=I X, where X is the impedance of either the inductor or the capacitor in the tuned circuit at the resonant frequency. The secret lies in two facts: Firstly, the impedance of a reactive component, (inductor or capacitor), is “at right angles to” ordinary resistive impedance, (even though they are both measured in Ohms). Thus, although reactive ohms can be added or subtracted directly to or from other reactive ohms, they cannot be added or subtracted directly to or from resistive ohms. They can only be added or subtracted by using the “parallelogram of vectors” method. Secondly, the impedance of an inductor is conventionally positive, whereas that of a capacitor is negative. So capacitive impedance can subtract from inductive impedance and, at the resonant frequency, produce zero impedance. The end result is that at the resonant frequency of the tuned circuit, the current through the resistor, inductor and capacitor in series is just that limited by the resistor, even though the impedances of the inductor and the capacitor separately can be very high. Thus, for a modest current, the volts across either the inductor or capacitor separately can also be very high. As an example, figure 1 shows the RF voltage across either the inductor or the capacitor of a resonant circuit with a Q of 12, as the frequency of an input of 1Volt in series with the components is changed.

Although we have looked at ‘Q’ from the impedance point of view, fundamentally, Q is defined as; “The number of radians required for the stored energy in an isolated resonant circuit to decay to 1/e, (about 37%), of its initial value”. However, explaining “radians” and “e” is beyond the scope of this article except to say that each cycle of oscillation is equal to 2 Pie radians, Pie is about 3.14159, and e is the base of Natural Logarithms and its value is about 2.718282.

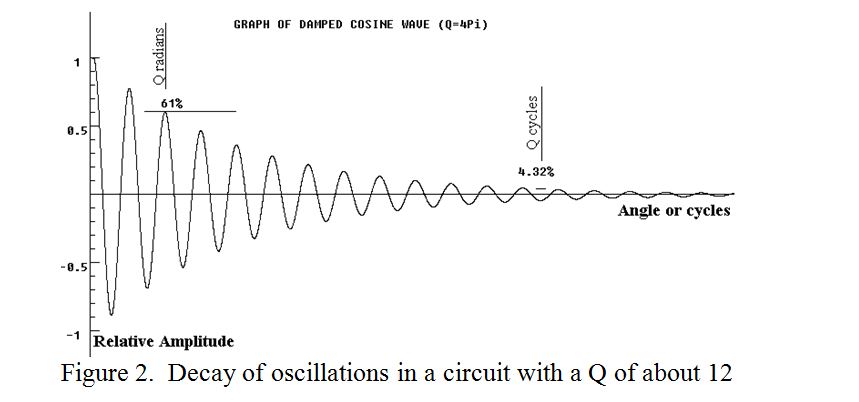
It is worth noting that after Q cycles, (as opposed to Q radians), the amplitude has fallen to less than 5% of its initial value, which in practice means that it can usually be taken to have died out. A little more maths reveals that the Q of a resonant circuit also determines its relative “bandwidth”, i.e. how it behaves when it is continuously energised at frequencies away from its resonant frequency. For Qs significantly greater than unity, the difference in frequency between the two “half power” points, (3dB points), of an “amplitude versus frequency plot”, divided by the peak or resonant frequency is equal to Q.

Only single resonant circuits can be defined by their Q. Two or more coupled resonant circuits have a more complicated response to an input frequency. They may have a relatively flat response over a restricted frequency band, or even a double or multi-humped response. Much use is made of coupled resonant circuits when designing various types of bandpass filter.

Back

         John,   G0NVZ