Derivation of Impedance for Minimum Loss
Back
In an air spaced coaxial cable, all the loss is associated with resistive loss in the central conductor and the surounding “outer”, sheath or braid. At radio frequencies the current is not uniformly distributed across the cross sectional area of the conductors but is confined to the oposing surfaces, hence loss is inversely proportional to the radii of the conductors and not to their cross sectional area. However, the larger the coax, the lower the loss.
The characteristic impedance of a coaxial cable is determined by the ratio of the radii, (or diameters), of the outer to the inner conductors, (Do/Di), where Do and Di are the diameters of the outer and inner conductors respectively. thus:-
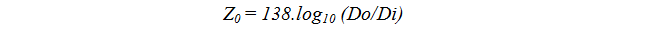
The loss per unit length of a coaxial cable is proportional to the “effective resistance of the centre conductor plus that of the outer conductor” compared to the characteristic impedance. Consider a coax of fixed size, i.e. of fixed outer diameter which for convenience is made unity. Di will always be smaller then Do, i.e. Di < 1.
It might be thought that raising the characteristic impedance would lower the loss as the conductor resistances would then be a smaller proportion in comparison to the characteristic impedance. However, raising the characteristic impedance for a fixed size of outer conductor entails reducing the diameter of the inner conductor which increases its loss. The loss per unit length of cable is therefore a function of both the resistances of the conductors and the characteristic impedance of the cable, Zo. The result of these two conflicting considerations is that there is a ratio at which the loss is a minimum.
It is the purpose of this note to find the value of Di and hence Zo which give the lowest loss for a fixed outer diameter of coax:-
Let the resistance of the inner conductor per unit length be Ri and that of the outer conductor be Ro. It is convenient to standardize the resistance of the outer conductor also to unity.
Ri 1/Di and Ro 1/Do. As Do and hence Ro are fixed at unity and only Di is varied we may write R 1 + 1/Di, where R is proportional to the total resistive loss.

| Back |
|---|
